In many automation systems, solving multivariable control problems using a single-variable PID controller involves transforming the multivariable problem into multiple single-variable feedback control loops. This approach can be broken down into two steps:
1. Pairing
The design of the control system first aims to balance the number of controlled variables with the number of manipulated variables. This process is called “pairing,” and it involves selecting the correct pairings of variables or combining variables as needed.
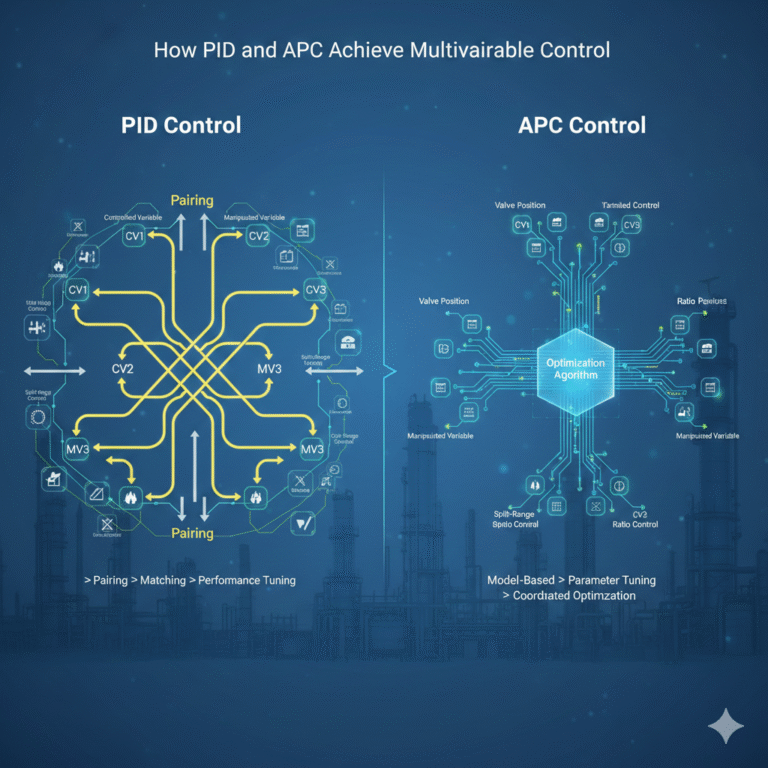
2. Matching
After the pairing process, each manipulated variable is assigned to a controlled variable, and PID single-loop controllers are implemented for feedback control.
The pairing process primarily involves control strategies such as valve position control, cascade control, and ratio control. While split-range control and override control are well-known, we recommend approaching these strategies with caution. When both split-range and override control are used together in a control scheme, there is often a simpler implementation available. Additionally, cascade control and feedforward control are not part of the pairing process but are considered later to improve control performance.
Matching principles during pairing include factors like strong relationships, fast dynamics, broad range, and independent causality. However, these criteria may not always be fully met, and in some cases, certain rules must be relaxed to achieve good performance. For example, nested control strategies rely on the coupling between loops. Once the pairings are determined, control performance can be optimized using various methods. If performance is insufficient, re-pairing may be considered.
APC: A Natural Approach to Multivariable Control
In contrast to PID control, Advanced Process Control (APC) naturally handles multivariable control. APC solves multivariable control problems by using an optimization-based approach. It only requires a control model between controlled variables and manipulated variables, without the need for pairing.
Through parameter setting, APC can simultaneously control multiple manipulated variables and controlled variables. This flexibility makes APC more cost-effective than PID in multivariable control. It satisfies the same variable structures while reducing the difficulty of modifying and implementing control schemes.
While PID can theoretically handle multivariable control, the complexity makes it difficult to widely adopt. APC, on the other hand, provides a simpler solution by using models and parameters to achieve multivariable control. Unlike PID, APC excels in multivariable coordination and optimization.
Although APC can use linear models, its true strength lies in coordinating and optimizing multiple variables. For APC, the model and variables are fixed, and by adjusting parameters, it can perform valve position control, cascade control, ratio control, split-range control, etc. These strategies, when implemented using PID, would require different configurations, with each one tailored for a specific application.

Conclusion
While PID control can be used for multivariable control, its complexity and limitations make it challenging to apply broadly in real-world scenarios. APC provides a more efficient and flexible approach to multivariable control, reducing the need for complex pairing and enabling better optimization across multiple variables.
