Introduction
For many years, differential pressure meters were the only devices available for measuring volumetric flow rate in a pipe with reasonable accuracy at a reasonable cost. Nowadays there are many alternatives, but even so, the differential pressure meter family still holds the largest slice of the market.
Advantages
The popularity of differential pressure meters is probably due to the following collection of advantages.
(a) Simplicity of construction: there are no moving parts to go wrong inside the pipe, and any electrical readout equipment is wholly on the outside of the pipe where it can be easily serviced.
(b) Versatility: they can be used with almost any fluid, from superheated steam to sulphuric acid.
(c) Economy: by choosing the right kind of differential pressure meter, one can have either a low initial cost or a low head loss and hence low pumping cost-but not both together.
(d) Experience: there is an abundance of published information, and of advice enshrined in codes of practice, relating to differential pressure meters used in very many different ways.
Disadvantages
(a) The accuracy is not quite as high as that of some of the more modern types of meter-especially if, as is commonly the case, the differential pressure meter is sold without calibration for the sake of cheapness. (The actual accuracies obtainable depend on circumstances, but as a very rough guide figures of ±1% if calibrated and ±2 or 3% if uncalibrated may be borne in mind)
(b) The output signal, differential pressure, is not linear with flow rate but is proportional to Qv2. This not only necessitates the extraction of a square root every time a reading is taken (which is no great problem with modern data processors) but, more seriously, it means that the rangeability of this type of flowmeter is generally much lower than that of flowmeters with a linear output.
Basic Principles
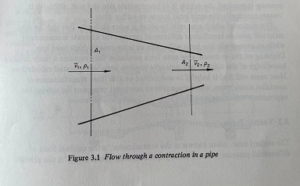
The meter depends upon the fact that when a fluid flows through a contraction it must accelerate; this causes its kinetic energy to increase, and consequently, its pressure must fall by a corresponding amount, in accordance with the principle of the conservation of energy. In Figure 3.1, fluid at a mean velocity, v1, and density, p1, passes a cross-section of area, A1, then it passes the smaller cross-section, A2, at v2 and p2.
By applying both Bernoulli’s equation and the principle of continuity (see section 1.2.5) between the two cross-sections, it can be shown that for an ideal and incompressible fluid
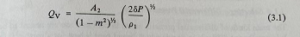
Where m is the “area ratio”, A2/A1, and p is the measured “differential pressure” (P1-P2) between the two cross-sections.
Unfortunately, real fluids are not ideal, and an empirical coefficient, C, known as the “coefficient of discharge”, must be introduced to allow for this. Also, if the fluid is a gas, a second empirical coefficient, the “expansibility factor”, e, must be introduced. This depends upon the physical properties of the gas being metered, as well as the geometry of the flow meter. The equation for practical use then becomes
If the highest possible accuracy is required, the coefficient, C, must be obtained by calibrating the meter over a range of flow rates. Where an accuracy around ±2% is acceptable, values of C for each type of meter can be obtained from national1 and national 2 standard specifications; tabulated values of e are obtainable from them, too. These standards also specify the main geometrical requirements for each type of meter and provide standard methods for calculating the uncertainty(accuracy) likely to be obtained under various conditions of use.
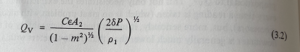
A complete differential pressure meter consists of two parts: the piece that fits into the pipe and generates the differential pressure is known as the “primary” whilst the associated device for measuring the differential pressure is called the “secondary”. This chapter is concerned only with various types of primary devices, while secondary devices are dealt with in Chapter 12.
Selecting a differential pressure meter
The main kinds of differential pressure meters in common use are described below. It is usually not difficult to decide which broad type is best for a particular job. The lengthy, expensive venturi meter has a low head loss and its high initial cost is therefore justified in situations where large quantities of liquid are being pumped more or less continuously-for example, in main water supply pipelines. Where head loss is not very important, as is often the case in process plants and in gas lines, the cheapness of the orifice plate is the decisive factor. If a compromise is required, the nozzle is of intermediate size and cost, although it creates practically the same head loss as an orifice plate.
The choice of which area ratio to adopt is more difficult. Too high an area ratio will provide insufficient differential pressure for accurate measurement, while an excessively low ratio will create an unnecessarily high head loss.
Deciding on the optimum area ratio for a particular duty requires fairly detailed knowledge of the subject, and generally involves some complicated calculations. Most users will find it helpful to seek advice on this from manufacturers or specialist consultants, who have access to computer programs for solving the appropriate equations speedily.
