I have gradually come to realize that, when it comes to PID tuning methods, the most important factors are not performance, but simplicity and universality. The Lambda tuning method, after a series of improvements, possesses characteristics that are more suitable for engineering applications. Unlike traditional PID methods, Lambda tuning does not use derivative action, instead relying on PI control for self-regulating processes. Furthermore, the integral time is set equal to the equivalent time constant, and by simply adjusting the proportional gain, the desired closed-loop performance can be achieved.
Frequency-domain analysis can explain why the Lambda tuning method consistently delivers good closed-loop performance. The proportional gain calculation is related to the characteristics of the controlled system, and Lambda tuning does not use model identification techniques. Instead, it draws from the Ziegler-Nichols (ZN) method, where system characteristics are determined through graphical methods. Like ZN, it is simple, but the characteristic curve is different from ZN’s response curve. The system characteristic obtained is not the actual model of the process but rather a control model requiring only three parameters: equivalent gain, equivalent time constant, and equivalent pure delay.
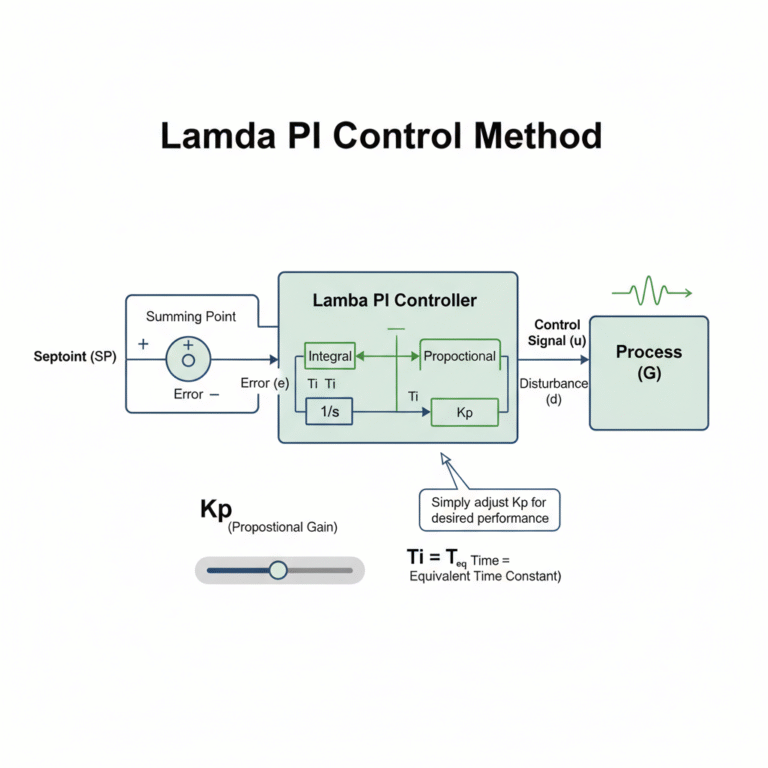
Lambda tuning is widely applicable to processes with inherent monotonic behavior, including systems with large time constants, large pure delays, multiple time constants, and reverse processes. Its PI controller is suitable for most industrial systems. The main advantage of the Lambda method lies in its simplicity and broad applicability.
For self-regulating systems, the Lambda tuning method works as follows (see diagram). However, since Lambda tuning does not use derivative action and fixes the integral time, it does sacrifice some performance. This is the main disadvantage of the Lambda tuning method.
For Integral Systems
An integral system is essentially a self-regulating system with an infinite time constant. Using Lambda tuning on such a system results in a purely proportional controller. Both industrial practice and theory have shown that even for integral systems, the purely proportional control provided by Lambda tuning still leaves a steady-state error. This issue must be addressed by adding a reasonable amount of integral action. The result is twofold: 1) the steady-state error is eliminated, and 2) overshoot occurs when setpoints change. In practice, for integral systems, a PI controller with a proportional-first approach becomes a viable option.
For Pure Delay Systems
For pure delay systems, which have a time constant of zero, Lambda tuning produces a purely integral controller. In such cases, there is significant room for performance improvement. To further enhance performance, alternative tuning methods must be used. A feasible tuning method is the use of a proportional gain lower bound of 1/(4K).
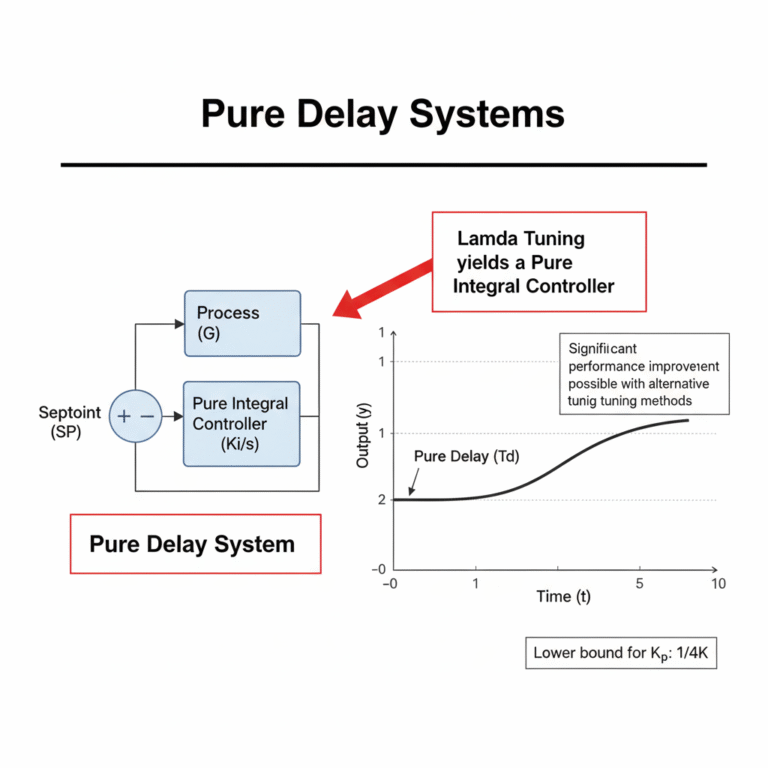
For Large Time Constant Systems
When the pure delay is small, Lambda tuning results in a large proportional gain PI controller. However, this controller may exceed physical limits, and increasing the proportional gain may be impractical. A simple reduction in the proportional action could lead to insufficient disturbance rejection. In such cases, enhancing the integral action is one potential solution. However, this adjustment would no longer be in line with Lambda tuning.
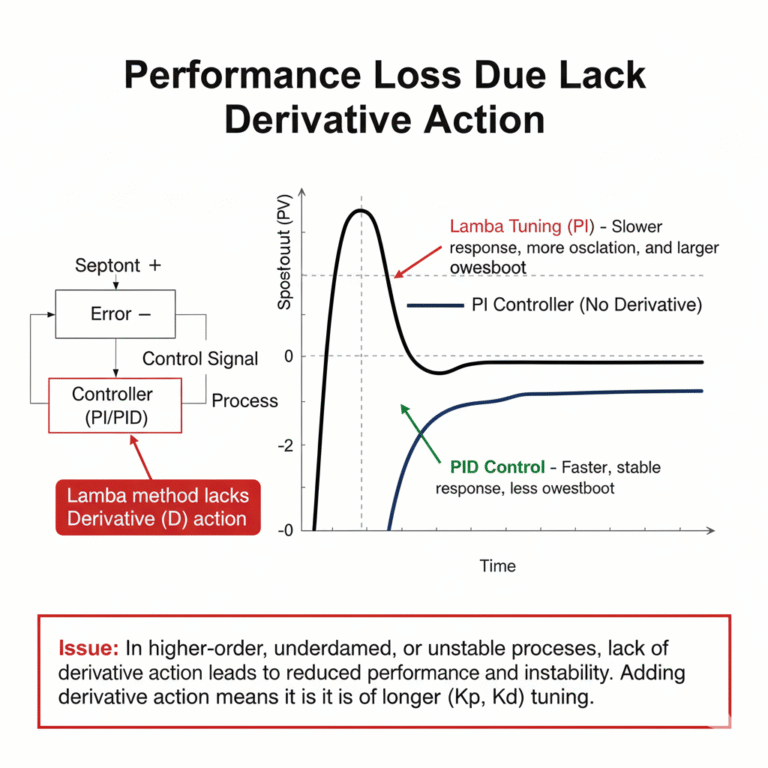
Performance Loss Due to Lack of Derivative Action
Lambda tuning does not use derivative action, and this can result in performance loss, especially in higher-order processes. For underdamped or unstable processes, the inclusion of derivative action becomes essential, which renders the Lambda method ineffective in such cases. Once derivative action is added, it no longer follows the Lambda tuning approach.
Conclusion
Among these four issues, the integral system is the most common in industrial processes and must be carefully considered. The other three issues are rare in industrial settings, so making the tuning method more complex for these issues is unnecessary. These three cases should be treated as special exceptions, with specific PID parameter settings applied.
