In the field of instrumentation and process control, theory is like a wrench—it may seem insignificant, but when it matters, it’s essential. Whether for obtaining basic certification or for daily tasks, concepts such as circuit diagrams, sensor principles, and troubleshooting are crucial. This series will continue to update, helping you master theoretical knowledge while providing a solid foundation for practical work. By investing even a little time, you can build a strong grasp of the essentials. Let’s break down complex concepts and improve our practical skills step by step.
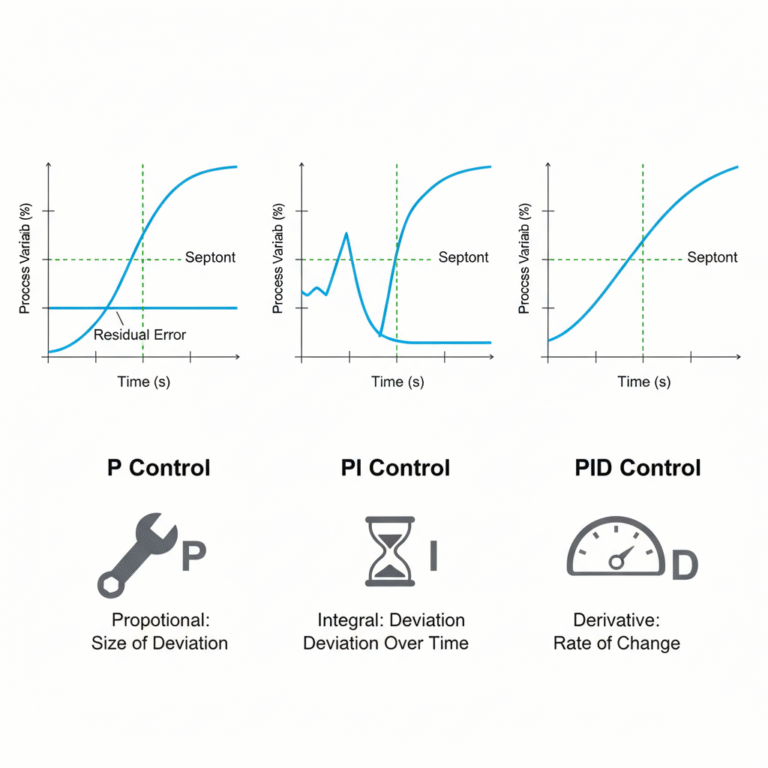
What Are Proportional (P), Integral (I), and Derivative (D) Control Laws?
What Role Do They Play in Automatic Control?
Proportional Control (P): The control action is based on the “size of the deviation.” The output is proportional to the input deviation. Proportional control is quick and powerful but can leave residual error. The strength of the control action is represented by the proportional gain (denoted as δ), where a higher gain results in stronger control. However, too strong of a proportional action can lead to oscillations.
Integral Control (I): This is based on whether the deviation exists over time. The output is proportional to the integral of the deviation. The integral action eliminates the residual error, but it increases the maximum deviation and prolongs the adjustment time. The strength of the integral action is represented by the integral time (Ti), where a shorter Ti leads to stronger action. However, too strong of an integral action can also cause oscillations.
Derivative Control (D): This is based on the “rate of change” of the deviation. The output is proportional to the rate of change of the deviation. It works by preventing the controlled variable from changing too quickly, offering anticipatory control. Derivative control is effective for systems with large delays. It helps reduce the deviation and shorten the response time but cannot eliminate it entirely. The strength of the derivative action is represented by the derivative time (Td), where a larger Td strengthens the effect. However, excessive Td can also lead to oscillations.
When Should You Use Proportional (P), Proportional-Integral (PI), or Proportional-Integral-Derivative (PID) Control?
Proportional Control (P): Suitable for systems with small load changes, minimal pure time delay, and where some residual error is acceptable. The process does not require very high precision.
Proportional-Integral Control (PI): Suitable for systems with small time constants and large load changes, where residual errors caused by disturbances need to be eliminated. The time constant is not large, and no significant deviation from the set point is allowed.
Proportional-Integral-Derivative Control (PID): Suitable for systems with significant time delays, moderate load changes, and where residual errors are not permissible.
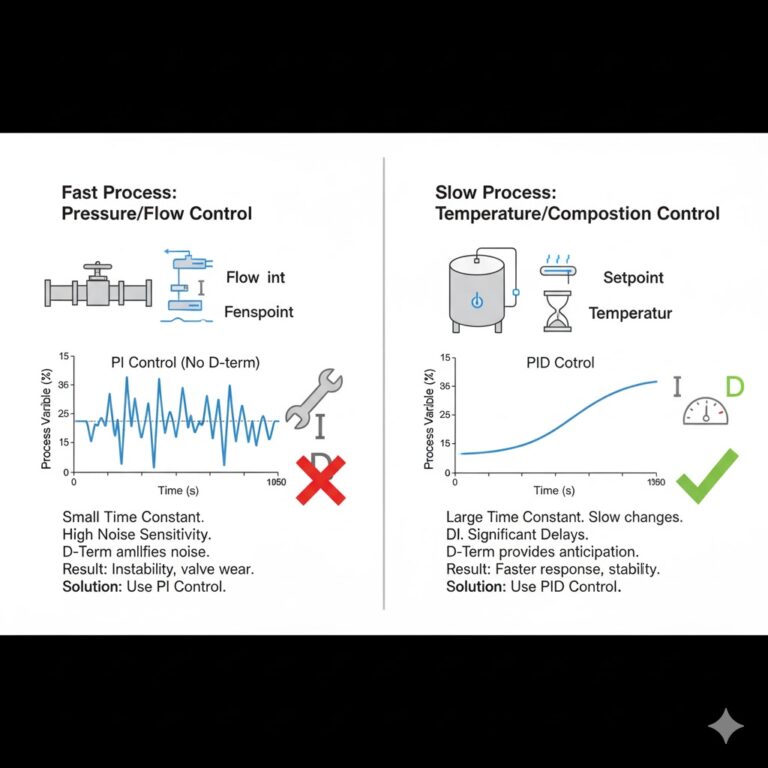
Why Don’t Pressure and Flow Control Typically Use Derivative Control, While Temperature and Composition Control Often Do?
For variables like pressure and flow, the system’s time constant (To) is typically small, and the load changes rapidly. In such cases, both the derivative and integral actions can cause oscillations, significantly affecting the control quality. Therefore, derivative control is generally not employed for pressure and flow regulation.
On the other hand, temperature and composition systems usually have larger time constants in both the measurement and control loops. In such systems, the anticipatory nature of derivative control proves effective, helping to improve control quality by mitigating excessive variations and speeding up the system’s response.
Does Introducing Derivative Action Improve Furnace Exit Temperature Control?
Yes, introducing derivative action can allow for smaller proportional gains and shorter integral times, improving control performance. The anticipatory nature of derivative control prevents excessive variations, thereby improving system stability. By reducing the proportional gain and shortening the integral time, the maximum deviation can be minimized, and the residual error can be eliminated more quickly.
However, it’s important to adjust these parameters appropriately when modifying the controller settings. Introducing derivative action can reduce the necessary proportional gain and integral time, thus achieving better control quality without compromising the system’s stability.
