Temperature and Pressure Compensation in Vortex Flowmeters - Just Measure it

Temperature and Pressure Compensation in Vortex Flowmeters

/ Flow meter

Abstract

Vortex flowmeters are widely used for measuring gas, steam, and liquid flows in industrial processes. Since vortex flowmeters measure operating (actual) volume flow, temperature and pressure compensation is required under certain conditions to ensure accuracy. This article explains when compensation is necessary, the underlying principle of density correction, the sequence of compensation steps, and the related technical standards. Practical diagrams and calculation examples are also suggested for clarity.

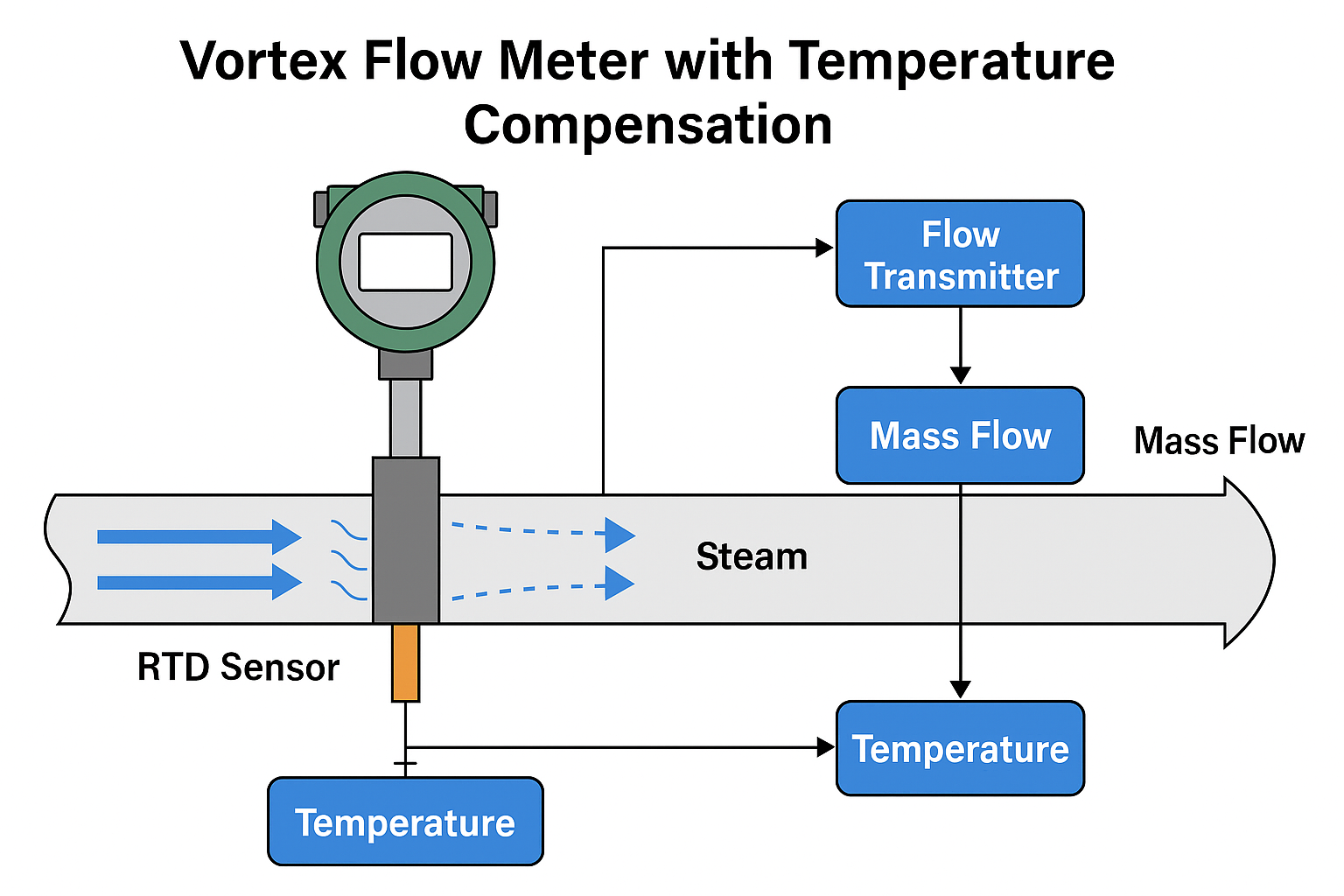
1. When Temperature and Pressure Compensation is Required

Vortex flowmeters measure the operating volume flow of the medium. Compensation is required in the following cases:

  • For gases
    Gas volume changes significantly with temperature and pressure. If operating conditions deviate from the design conditions, gas density changes, making the measured volume flow unrepresentative of actual mass flow or standard volume flow.

  • For superheated steam
    The density of superheated steam is strongly dependent on temperature and pressure. Operating condition changes cause large density variations. Compensation is therefore essential to obtain accurate mass flow or energy flow.

  • For liquids (e.g., water, oil) or saturated steam
    Density changes due to temperature and pressure are minimal. Compensation is generally unnecessary.

Table 1 — Media Type vs. Compensation Requirement

Medium TypeDensity Sensitivity to T/PCompensation RequiredNotes
GasHighYesStrongly affected by both temperature and pressure; must correct to obtain accurate mass or standard volume flow.
Superheated SteamHighYesFar from saturation line; density depends strongly on T and P; required for mass/energy flow accuracy.
Saturated SteamLowGenerally NoDensity variation with T/P is small near saturation; usually negligible in engineering applications.
Liquid (e.g., water, oil)Very LowNoDensity changes slightly with T/P; compensation normally unnecessary.

2. Principle of Compensation: Density Correction

The vortex flowmeter output (frequency, f) is proportional to the operating volume flow (Q).
Basic formula:

Q=fKQ = \frac{f}{K}

Where:

  • Q = operating volume flow

  • f = vortex shedding frequency

  • K = instrument factor (calibration constant)

However, users often need mass flow (Qm) or standard volume flow (Qn):

Qm=ρ⋅QQ_m = \rho \cdot Q Qn=Q⋅ρρnQ_n = Q \cdot \frac{\rho}{\rho_n}

Where:

  • ρ\rho = operating density (function of T, P)

  • ρn\rho_n = density at standard conditions

Thus, by measuring temperature (T) and pressure (P) in real time, the current operating density ρ\rho can be calculated (via the equation of state). The measured volume flow Q can then be corrected to obtain accurate mass flow or standard volume flow.

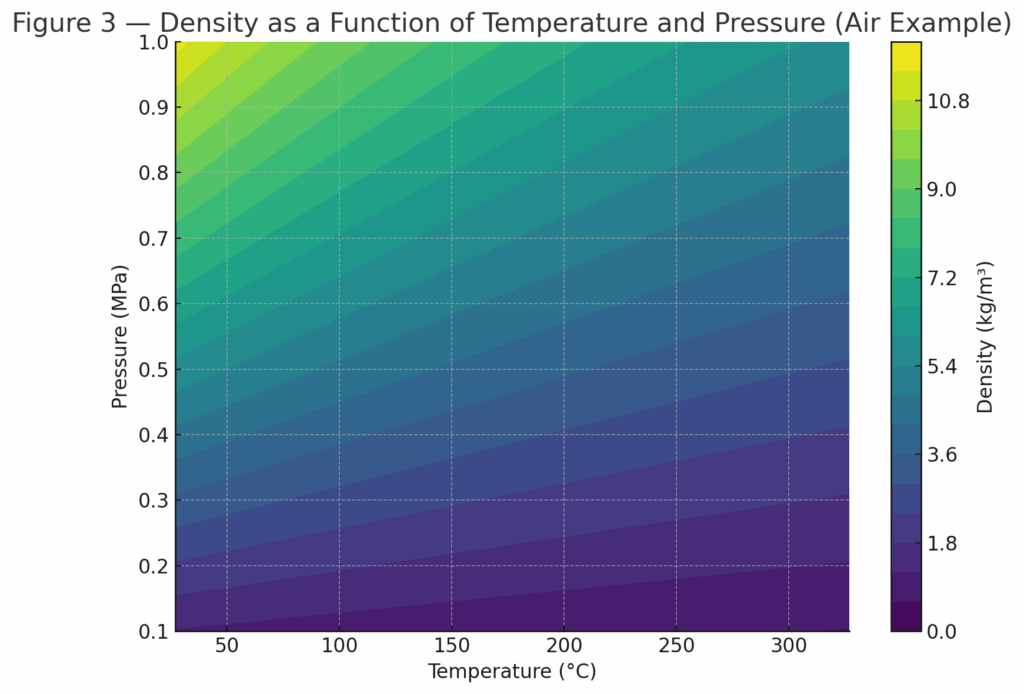
3. Sequence of Compensation and Standards Basis

3.1 Compensation Order

The conventional sequence is “pressure first, then temperature”:

  • For steam and most gases, pressure has a greater effect on density than temperature.

  • In engineering practice and flow totalizers, the density is first corrected by pressure, then refined by temperature.

📌 Figure 4 — Flow Compensation Logic Diagram (Pressure First → Temperature Second)

3.2 Standards and References

This practice is not defined in a single GB standard, but is embedded in national metrology and thermophysical property standards:

  • JJG 1029-2007 Verification Regulation of Vortex Flowmeters

  • GB/T 11062-2020 Natural Gas—Calculation of Calorific Value, Density, Relative Density and Wobbe Index

  • GB/T 10586-2006 Thermophysical Properties of Steam

These standards specify calculation models where density is derived from pressure and temperature. The calculation inherently follows a “pressure-priority” or “simultaneous T-P” principle.

4. Practical Example

Case:

  • Medium: Air

  • Pressure: 0.6 MPa

  • Temperature: 80 °C

  • Operating volume flow (Q): 100 m³/h

Steps:

  1. Use the state equation to calculate density ρ\rho at 0.6 MPa, 80 °C.

  2. Compute mass flow Qm=ρ⋅QQ_m = \rho \cdot Q.

  3. Calculate standard volume flow Qn=Q⋅(ρ/ρn)Q_n = Q \cdot (\rho / \rho_n).

Table 2 — Example Calculation: Air Flow at Different Conditions

Assumptions: ideal gas (compressibility Z≈1Z \approx 1); standard state Pn=101.325 kPa, Tn=20∘C=293.15 KP_n=101.325\ \text{kPa},\ T_n=20^\circ\text{C}=293.15\ \text{K}; air density at standard state ρn≈1.204 kg/m3\rho_n \approx 1.204\ \text{kg/m}^3.
Given: Vortex meter operating volume flow Q=100 m3/hQ=100\ \text{m}^3/\text{h}.

ρ=ρn⋅PPn⋅TnT,Qm=ρ⋅Q,Qn=Q⋅ρρn=Q⋅PPn⋅TnT\rho = \rho_n \cdot \frac{P}{P_n}\cdot \frac{T_n}{T},\qquad Q_m=\rho\cdot Q,\qquad Q_n=Q\cdot \frac{\rho}{\rho_n}=Q\cdot \frac{P}{P_n}\cdot \frac{T_n}{T}

CaseMediumOperating Pressure PPOperating Temp. TTOperating Density ρ\rho (kg/m³)Mass Flow QmQ_m (kg/h)Standard Vol. Flow QnQ_n (Nm³/h)
AAir0.30 MPa (abs)80 °C (353.15 K)2.96296246
BAir0.60 MPa (abs)80 °C (353.15 K)5.92592492

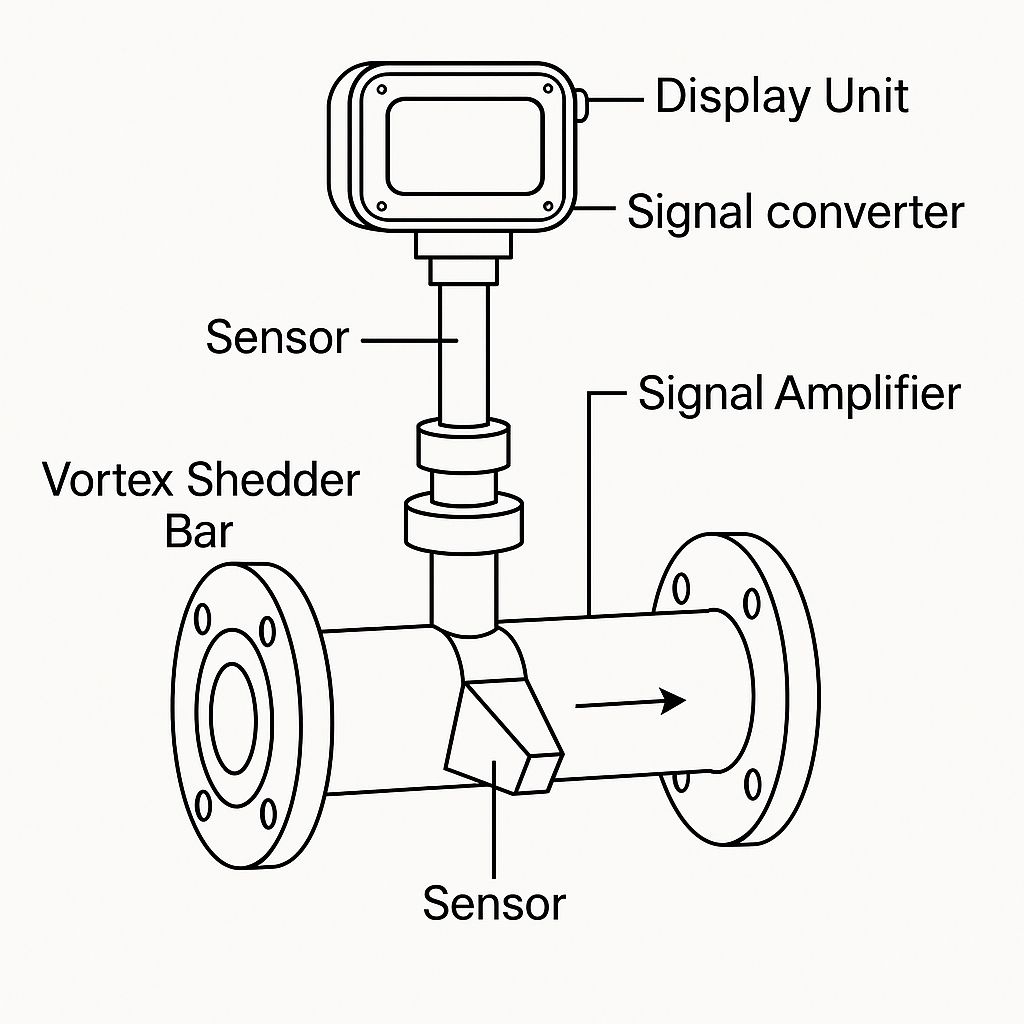
5. Conclusion

  • Temperature and pressure compensation is mandatory when measuring gases or superheated steam with vortex flowmeters.

  • The principle is to correct the density based on real-time temperature and pressure values.

  • The industry follows the “pressure-first, then temperature” rule, which aligns with the calculation logic in national metrology standards (JJG 1029, GB/T 11062, GB/T 10586).

  • In practice, flow totalizers and compensation modules integrate this correction logic automatically, ensuring accurate measurement of mass flow or standard volume flow.

Share This Story, Choose Your Platform!

Contact Us

    Please prove you are human by selecting the house.
    Request a Quote
    Translate »